5.2.2 Das hexagonale Porensystem

Damit Transportprozesse zwischen den Porenzellen modelliert werden können, müssen die Nachbarschaftsbeziehungen eindeutig definiert sein. Dazu muss ihnen ein Koordinatenpaar im zweidimensionalen Raum zugeordnet werden Für ein hexagonales Gitter, ergeben sich theoretisch mehrere Möglichkeiten. Hier werden die Hexagone in $y$-Richtung von unten nach oben und in $x$-Richtung von links nach rechts nummeriert (5.2).

Abbildung 5.2: Nummerierung der Koordinaten eines hexagonalen Systems

Die einzelnen hexagonalen Porenzellen sind in einem Gittersystem angeordnet. Dieses hat die Form eines Trapezes um den realen Gegebenheiten in der Kompostmiete möglichst nahe zu kommen. Ein Trapez wird durch die Variablen X_BOTTOM, X_TOP und Y_HEIGHT beschrieben(5.3). Im Modell werden diese Daten zu Beginn der Simulation aus einer Eingabedatei eingelesen.

Abbildung: Maße eines Trapezes

Die Wahl der Seitenlänge eines Hexagons bestimmt, wie die einzelnen Zellen in dem trapezförmigen Gitter ausgerichtet werden. Die Anzahl der Gitterreihen in $y$-Richtung lassen sich mit Formel 5.2 berechnen. Allerdings ist die räumliche Ausdehnung der Zellen in $y$-Richtung nicht einfach ein Vielfaches von HEX$_Y$. In Abbildung 5.2 wird deutlich, dass die vertikalen Zellreihen um den Faktor HEX $* \sin(60^\circ)$ oder $\frac{1}{2}*\mathtt{HEX}_Y$ versetzt sind, sobald $X>1$ ist. Für die Ausdehnung in $y$-Richtung ergibt sich bei einer gegebenen Anzahl von horizontalen Reihen (ROWS):

$$\ \ \mathtt{Y\_HEIGHT} = \mathtt{ROWS} * \mathtt{HEX}_Y + \mathtt{HEX} *\sin(60^\circ) , X>1$$ (5.7)

oder

$$\ \ \mathtt{Y\_HEIGHT} = \mathtt{HEX}_Y * (\mathtt{ROWS} + 0,5) , X>1$$ (5.8)

Im Modell muss die Anzahl von ROWS aus der vertikalen Ausdehnung der Miete berechnet werden. Dazu kann die Formel 5.7 einfach umgeformt werden. Hierbei ist zu beachten, dass eine Transformation einer reellen Zahl zu einer ganzen Zahl stattfindet. SIMULA rundet das Ergebnis standardmäßig auf oder ab.

$$\ \ \mathtt{ROWS} = \frac{\mathtt{Y\_HEIGHT}}{\mathtt{HEX}_Y} - \mathtt{HEX} * \sin(60^\circ)$$ (5.9)

Die Anzahl der $X$-Zellen richtet sich nach der Breite des Trapez in der jeweiligen $Y$-Reihe. Im Folgenden wird ein mögliches Berechnungsverfahren vorgestellt, das auch im Modell benutzt wird.

Unter Zuhilfenahme von Formel 5.1 kann die Anzahl von X-Zellen in einer bestimmten Y-Reihe bestimmt werden. Das Maximum liegt bei X_BOTTOM und das Minimum entsprechend bei X_TOP.

$$\ \ \mathtt{X\_CELLS}_{max} = \frac{2}{3}*\biggl(\frac{\mathtt{X\_BOTTOM}}{\mathtt{HEX}} - 0,5\biggr)$$ (5.10)

$$\mathtt{X\_CELLS}_{min} = \frac{2}{3}*\biggl(\frac{\mathtt{X\_TOP}}{\mathtt{HEX}} - 0,5\biggr)$$ (5.11)

Die Anzahl der $X$-Zellen in den jeweilige Reihen liegt zwischen X_CELLS$_{max}$ und X_CELLS$_{min}$. Im Modell wird sie durch die Prozedur UPDATE_X berechnet. Diese erhält als Input-Parameter die $Y$-Reihe, in der die Zellen generiert werden sollen. Daraus wird zunächst berechnet, in welcher realen Höhe sich die Reihe befindet:

$$\ \ \mathtt{Y\_UPD} = \mathtt{Y\_HEIGHT}_{max} - \mathtt{HEX}_Y * (\mathtt{ROWS} + 0,5)$$ (5.12)

Anschließend wird ermittelt wie weit sich die zu generierende Reihe in der $X$-Richtung ausdehnt(X_INT). Aus dem Strahlensatz ergibt sich (Abb. 5.4):

$$\ \ \mathtt{X\_UPD} = \mathtt{Y\_UPD} * \frac{0.5 * (\mathtt{X\_BOTTOM} - \mathtt{X\_TOP)}}{\mathtt{Y\_HEIGHT}}$$ (5.13)

und

$$\mathtt{X\_INT} = 2 * \mathtt{X\_UPD} + \mathtt{X\_TOP}$$ (5.14)

Abbildung: Linker Seitenflügel eines Trapez. Unter Zuhilfenahme des Strahlensatzes kann aus den geometrischen Verhältnissen X_UPD berechnet werden

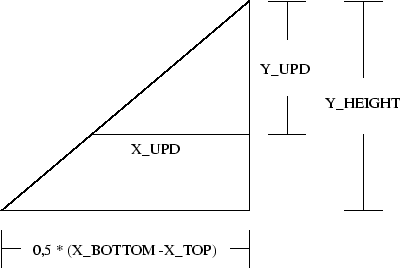Die Anzahl der Zellen wird wie in den Formeln 5.10 und 5.11 berechnet:

$$\mathtt{X\_CELLS}_{int} = \frac{2}{3}*\biggl(\frac{\mathtt{X\_INT}}{\mathtt{HEX}} - 0,5\biggr)$$ (5.15)

Schließlich müssen die Koordinaten der $X$-Zellen noch zentralisiert werden. Dazu dient die Prozedur CENTRALIZE, die als Input-Parameter X_CELLS$_{int}$ erhält. Ohne den Aufruf von CENTRALIZE würden sich die Zellen am linken Rand des Gittersystems anordnen, es ergäbe sich dann kein Trapez.

In der Prozedur wird zunächst ermittelt, wie viele Zellen im gesamten Koordinatenraum $(1,\dots,X;1,\dots,Y)$ vor und hinter den Zellen im Trapez nicht generiert werden sollen:

$$\ \mathtt{X\_NI}_{\textit{in front of trapez}} = \frac{ \mathtt{X\_CELLS}_{max} - \mathtt{X\_CELLS}_{int}}{2}$$ (5.16)

$$\mathtt{X\_NI}_{\textit{after trapez}} = \mathtt{X\_NI}_{\textit{in front of trapez}} + \mathtt{X\_CELLS}_{int}$$ (5.17)

Die Werte X_NI $_{\textit{in front of trapez}}$ und(X_NI $_{\textit{after trapez}}-1)$ dienen nun als Grenzparameter einer Schleife, welche die Porenzellen sukzessiv initiiert.

Abbildung 5.5 stellt beispielhaft ein mit den oben beschriebenen Verfahren generiertes Porensystem dar.

Abbildung 5.5: Beispiel einer Modellmiete, die mit folgenden Werten generiert wurde: HEX = 0,1m, X_TOP = 1m, X_BOTTOM = 4m, Y_HEIGHT = 2m.

In dieser Abbildung wird allerdings nicht deutlich, dass um die Modellmiete herum weitere Zellen als Grenzbedingungen definiert werden müssen. Die Luftoberfläche und der Untergrund werden durch Gitterzellen definiert, die durch konstante Parameterwerte gekennzeichnet sind. An der Boden-Luft Grenze finden Diffusionstransportprozesse in die Miete hinein statt, wobei die Sauerstoffkonzentration in den Luftzellen konstant bleibt. Mit den Untergrundzellen finden keine Austauschvorgänge statt. Die Grenzzellen außerhalb der Modellmiete werden zwar als Objekte initiiert, sie werden jedoch nicht wie die Porenzellen aktiviert. Berechnungen finden ausschließlich in aktivierten Objekten statt.

Für jede Porenzelle in der Versuchsmiete müssen die Nachbarschaftsbeziehungen genau definiert sein. Aus Abbildung· 5.2 ist ersichtlich, dass die Bestimmung der Koordinaten für jeden der sechs Nachbarn nicht so trivial ist, wie bei einem viereckigen Gittersystem. Tabelle 5.1 zeigt, dass die Berechnung der Koordinaten der angrenzenden Zellen sich zwischen geraden und ungeraden $x$-Werten unterscheidet.

Tabelle 5.1: Nachbarschaftsbeziehungen einer Zelle mit den Koordinaten ($x$;$y$). Zur Veranschaulichung siehe Abb. 5.2

		$x$ gerade	$x$ ungerade
oben		$x$	$y+1$	$x$	$y+1$
unten		$x$	$y-1$	$x$	$y-1$
rechts oben		$x+1$	$y+1$	$x+1$	$y$
rechts unten		$x+1$	$y$	$x+1$	$y-1$
links oben		$x-1$	$y+1$	$x-1$	$y$
links unten		$x-1$	$y$	$x-1$	$y-1$

Die Differenzierung zwischen geraden und ungeraden $x$-Werten wird im Modell durch den modulo-Befehl erreicht. Damit wird der Rest der Division einer ganzen Zahl durch eine andere bestimmt. Ist das Ergebnis von mod($x$,2) gleich Null, ist $x$ gerade, sonst ungerade. Nach Unterscheidung dieser beiden Fälle werden die Nachbarn einer Zelle mit den Koordinaten ($x$,$y$) mit der Prozedur UPDATE_NEIGHBORS ermittelt.